Model and Cost Function in Machine Learning
When the target variable that we’re trying to predict is continuous, such as in our housing price example, we call the learning problem a regression problem. Lets take a Regression problem and go through how the Model and Cost functions works under the hood
Model Representation
To describe the supervised learning problem slightly more formally, our goal is, given a training set, to learn a function h : X → Y so that h(x) is a “good” predictor for the corresponding value of y. For historical reasons, this function h is called a hypothesis. Seen pictorially, the process is therefore like this:
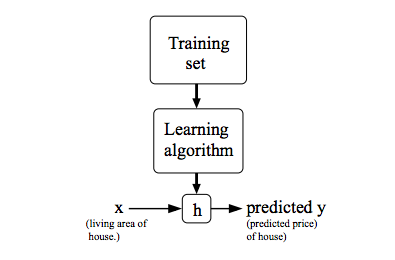
In this example, once we trained our model, we get the machine learning function h(x). Once you input x, it will predict the value of y
Training a Machine Learning Model
Training a model simply means learning (determining) good values for all the weights and the bias from labeled examples. In supervised learning, a machine learning algorithm builds a model by examining many examples and attempting to find a model that minimizes loss; this process is called empirical risk minimization
Loss is the penalty for a bad prediction. That is, loss is a number indicating how bad the model's prediction was on a single example. If the model's prediction is perfect, the loss is zero; otherwise, the loss is greater. The goal of training a model is to find a set of weights and biases that have low loss, on average, across all examples. For example, Figure 3 shows a high loss model on the left and a low loss model on the right. Note the following about the figure:
- The arrows represent loss.
- The blue lines represent predictions.
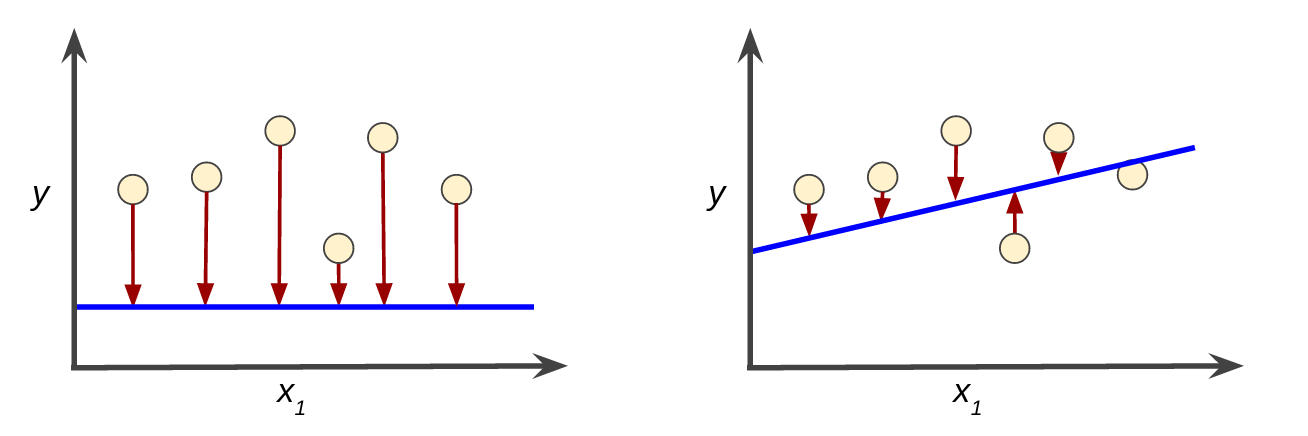
Clearly, the line in the right plot is a much better predictive model than the line in the left plot
Cost Function (aka Loss Function)
We can measure the accuracy of our hypothesis function by using a cost function. This takes an average difference (actually a fancier version of an average) of all the results of the hypothesis with inputs from x's and the actual output y's
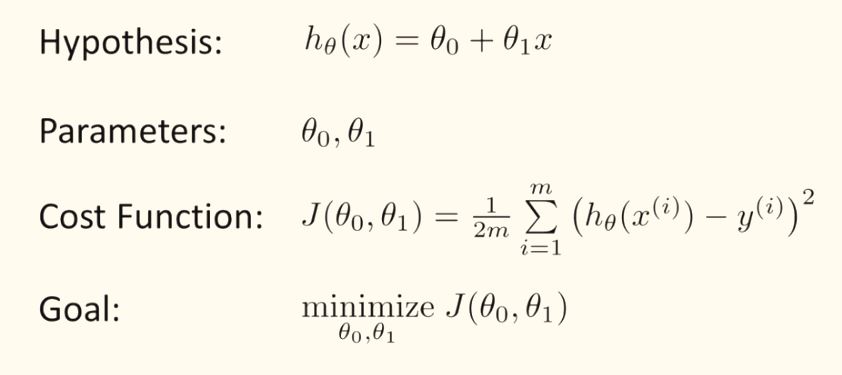
This function is otherwise called the "Squared error function", or "Mean squared error". The mean is halved as a convenience for the computation of the gradient descent, as the derivative term of the square function will cancel out the half term